1. АНАЛИЗ ПОСТАНОВКИ ЗАДАЧИ 1.1 Постановка задачи. Разработать программу для определения минимума функции. Сравнить эф-фективность методов покоординатного и градиентного спуска. Продемонстри-ровать данные методы для функции

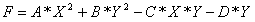
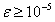
Исходные данные: значения коэффициентов (a, b, c, d), координаты начальной точки (x, y), погрешность . Выходные данные: значение минимума функции и количество итераций для методов покоординатного и градиентного спуска.

1.2 Критерии эффективности и качества разрабатываемой программы.

Обязательным требованием для данной программы является правиль-ность выполнения. Важный критерий - интуитивность работы с программой: она не должна вызывать у пользователя сложностей в поиске необходимых элементов интерфейса для управления процессом решения поставленной зада-чи. Необходимо избежать избыточности. Это означает, что пользователь дол-жен вводить только минимальную информацию для работы или управления программой. Необходимо использовать значения по умолчанию, чтобы мини-мизировать процесс ввода информации. Также нужно, чтобы система обеспе-чивала пользователя необходимыми инструкциями. Сообщения об ошибках должны быть полезны и понятны пользователю.

1.3 Описание метода решения задачи.

Метод покоординатного спуска:

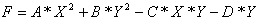
Программа фиксирует значение переменной X, таким образом по-лучается функция одной переменной Y. Считаются значения (1)

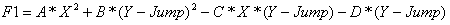
(2)

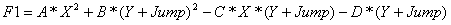
где Jump - шаг поиска. Если F1<F, то функция убывает в сторону убывания Y. Полагаем F=F1, дела-ем пересчет по формулам (1) и (2). Продолжаем движение по убыванию функ-ции до тех пор, пока сохраняется условие F1<F. Как только F1 становится больше F, уменьшаем шаг Jump вдвое, и начинаем движение в обратную сторо-ну пользуясь новой формулой для F1: (3)

Если F1 снова станет меньше чем F, то для расчета F1 надо будет опять поль-зоваться формулой (2). Так надо продолжать до пор, пока модуль разности |F-F1|> eps - допустимой погрешности.

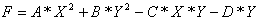
Затем программа фиксирует значение переменной Y, таким образом получается функция одной переменной X. Считаются значения (4)

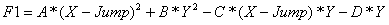
(5)

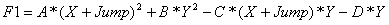
где Jump - шаг поиска. Если F1<F, то функция убывает в сторону убывания X. Полагаем F=F1, дела-ем пересчет по формулам (4) и (5). Продолжаем движение по убыванию функ-ции до тех пор, пока сохраняется условие F1<F. Как только F1 становится больше F, уменьшаем шаг Jump вдвое, и начинаем движение в обратную сторо-ну пользуясь новой формулой для F1: (6)

Если F1 снова станет меньше чем F, то для расчета F1 надо будет опять поль-зоваться формулой (5). Так надо продолжать до пор, пока модуль разности |F-F1|> eps - допустимой погрешности.

На этом поиск минимума методом покоординатного спуска окончен. F1 - минимум функции.

Метод градиентного спуска:

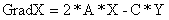
Программа вычисляет значение градиента данной функции в на-чальной точке. Градиент GradF - это сумма частных производных GradX+GradY. (7)

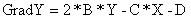
(8)

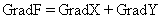
(9)

Если GradF=0, значит, функция убывает в сторону уменьшения координат. Полагаем

X-=Jump (10)
Y-=Jump (11)

Пересчитаем градиент.

Далее