|
Пример выполнения лабораторной работы по математике (2-й курс)
|
Лабораторная работа №1
Тема: "Решение нелинейных уравнений методом дихотомии"
Цель: "Научиться решать нелинейные уравнения с использованием математического пакета программных средств"
Задание: "Найти корень уравнения: (b+x^2)*(x-c)-e^a/(1-x^2)=С,
с точностью до 0,00005 при a=0.09; b=1.12; c=1.25."
> a:=0.09; b:=1.12; c:=1.25;
a := .09
b := 1.12
c := 1.25
> f:=x->(b+x^2)*(x-c)-exp(a/(1-x^2))-c;
2 a
f := x -> (b + x ) (x - c) - exp(------) - c
2
1 - x
> plot(f(x),x=-10..10,y=-10..10);
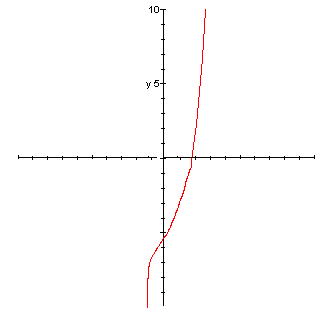
>
Первая итерация.
> n:=0;x1:=1.001;xr:=2;
n := 0
x1 := 1.001
xr := 2
> n:=n+1; xt:=(x1+xr)/2;
n := 16
xt := 1.769548310
> f(xt);f1:=f(xt)*f(x1);fr:=f(xr)*f(xt);
.000104917
-8
f1 := -.8256548232 10
-7
fr := .3027264626 10
> if f1<0 then xr:=xt else x1:=xt fi;
xr := 1.769548310
ў delta:=abs(xr-x1);
Если delta>=e, то требуемая точность не достигнута и снова выполняем команды, начиная со второй.
delta := .000030487
После 12 - й итерации получили, что длина последнего отрезка меньше е=0,0005. Следовательно за приближённое значение корня можно взять xt=1.769548310.
|
|
Содержание:
Лабораторная 1
Лабораторная 2
Лабораторная 3
Лабораторная 4
|

