Отношения, атрибуты, кортежи отношения

Определения и примеры

Фундаментальным понятием реляционной модели данных является понятие отношения. В определении понятия отношения будем следовать книге К. Дейта [11].

Определение 1. Атрибут отношения есть пара вида <Имя_атрибута : Имя_домена>.

Имена атрибутов должны быть уникальны в пределах отношения. Часто имена атрибутов отношения совпадают с именами соответствующих доменов.

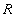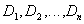Определение 2. Отношение , определенное на множестве доменов (не обязательно различных), содержит две части: заголовок и тело.

Заголовок отношения содержит фиксированное количество атрибутов отношения:

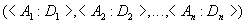
Тело отношения содержит множество кортежей отношения. Каждый кортеж отношения представляет собой множество пар вида <Имя_атрибута : Значение_атрибута>:

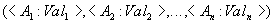
таких что значение 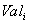атрибута 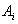принадлежит домену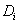

Отношение обычно записывается в виде:

,

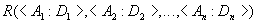или короче

,

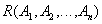или просто

.

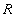Число атрибутов в отношении называют степенью (или -арностью) отношения.

Мощность множества кортежей отношения называют мощностью отношения.

Возвращаясь к математическому понятию отношения, введенному в предыдущей главе, можно сделать следующие выводы:

Вывод 1. Заголовок отношения описывает декартово произведение доменов, на котором задано отношение. Заголовок статичен, он не меняется во время работы с базой данных. Если в отношении изменены, добавлены или удалены атрибуты, то в результате получим уже другое отношение (пусть даже с прежним именем).

Вывод 2. Тело отношения представляет собой набор кортежей, т.е. подмножество декартового произведения доменов. Таким образом, тело отношения собственно и является отношением в математическом смысле слова. Тело отношения может изменяться во время работы с базой данных - кортежи могут изменяться, добавляться и удаляться.

Пример 1. Рассмотрим отношение "Сотрудники" заданное на доменах "Номер_сотрудника", "Фамилия", "Зарплата", "Номер_отдела". Т.к. все домены различны, то имена атрибутов отношения удобно назвать так же, как и соответствующие домены. Заголовок отношения имеет вид:

Сотрудники (Номер_сотрудника, Фамилия, Зарплата, Номер_отдела)

Пусть в данный момент отношение содержит три кортежа:

(1,Иванов, 1000, 1)

(2, Петров, 2000, 2)

(3, Сидоров, 3000, 1)

такое отношение естественным образом представляется в виде таблицы:

Таблица 1 Отношение "Сотрудники"

Определение 3. Реляционной базой данных называется набор отношений.

Определение 4. Схемой реляционной базы данных называется набор заголовков отношений, входящих в базу данных.

Хотя любое отношение можно изобразить в виде таблицы, нужно четко понимать, что отношения не являются таблицами. Это близкие, но не совпадающие понятия. Различия между отношениями и таблицами будут рассмотрены ниже.

Термины, которыми оперирует реляционная модель данных, имеют соответствующие "табличные" синонимы:

Свойства отношений

Свойства отношений непосредственно следуют из приведенного выше определения отношения. В этих свойствах в основном и состоят различия между отношениями и таблицами.

1. В отношении нет одинаковых кортежей. Действительно, тело отношения есть множество кортежей и, как всякое множество, не может содержать неразличимые элементы (см. понятие множества в гл.1.). Таблицы в отличие от отношений могут содержать одинаковые строки.
2. Кортежи не упорядочены (сверху вниз). Действительно, несмотря на то, что мы изобразили отношение "Сотрудники" в виде таблицы, нельзя сказать, что сотрудник Иванов "предшествует" сотруднику Петрову. Причина та же - тело отношения есть множество, а множество не упорядочено. Это вторая причина, по которой нельзя отождествить отношения и таблицы - строки в таблицах упорядочены. Одно и то же отношение может быть изображено разными таблицами, в которых строки идут в различном порядке.
3. Атрибуты не упорядочены (слева направо). Т.к. каждый атрибут имеет уникальное имя в пределах отношения, то порядок атрибутов не имеет значения. Это свойство несколько отличает отношение от математического определения отношения (см. гл.1 - компоненты кортежей там упорядочены). Это также третья причина, по которой нельзя отождествить отношения и таблицы - столбцы в таблице упорядочены. Одно и то же отношение может быть изображено разными таблицами, в которых столбцы идут в различном порядке.
4. Все значения атрибутов атомарны. Это следует из того, что лежащие в их основе атрибуты имеют атомарные значения. Это четвертое отличие отношений от таблиц - в ячейки таблиц можно поместить что угодно - массивы, структуры, и даже другие таблицы.

Замечание. Из свойств отношения следует, что не каждая таблица может задавать отношение. Для того, чтобы некоторая таблица задавала отношение, необходимо, чтобы таблица имела простую структуру (содержала бы только строки и столбцы, причем, в каждой строке было бы одинаковое количество полей), в таблице не должно быть одинаковых строк, любой столбец таблицы должен содержать данные только одного типа, все используемые типы данных должны быть простыми.

Замечание. Каждое отношение можно считать классом эквивалентности таблиц, для которых выполняются следующие условия:

• Таблицы имеют одинаковое количество столбцов.
• Таблицы содержат столбцы с одинаковыми наименованиями.
• Столбцы с одинаковыми наименованиями содержат данные из одних и тех же доменов.
• Таблицы имеют одинаковые строки с учетом того, что порядок столбцов может различаться.

Все такие таблицы есть различные изображения одного и того же отношения.

Первая нормальная форма

Труднее всего дать определение вещей, которые всем понятны. Если давать не строгое, описательное определение, то всегда остается возможность неправильной его трактовки. Если дать строгое формальное определение, то оно, как правило, или тривиально, или слишком громоздко. Именно такая ситуация с определением отношения в Первой Нормальной Форме (1НФ). Совсем не говорить об этом нельзя, т.к. на основе 1НФ строятся более высокие нормальные формы, которые рассматриваются далее в гл. 6 и 7. Дать определение 1НФ сложно ввиду его тривиальности. Поэтому, дадим просто несколько объяснений.

Объяснение 1. Говорят, что отношение 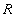находится в 1НФ, если оно удовлетворяет определению 2.

Это, собственно, тавтология, ведь из определения 2 следует, что других отношений не бывает. Действительно, определение 2 описывает, что является отношением, а что - нет, следовательно, отношений в непервой нормальной форме просто нет.

Объяснение 2. Говорят, что отношение 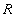находится в 1НФ, если его атрибуты содержат только скалярные (атомарные) значения.

Опять же, определение 2 опирается на понятие домена, а домены определены на простых типах данных.

Непервую нормальную форму можно получить, если допустить, что атрибуты отношения могут быть определены на сложных типах данных - массивах, структурах, или даже на других отношениях. Легко себе представить таблицу, у которой в некоторых ячейках содержатся массивы, в других ячейках - определенные пользователями сложные структуры, а в третьих ячейках - целые реляционные таблицы, которые в свою очередь могут содержать такие же сложные объекты. Именно такие возможности предоставляются некоторыми современными пост-реляционными и объектными СУБД.

Требование, что отношения должны содержать только данные простых типов, объясняет, почему отношения иногда называют плоскими таблицами (plain table). Действительно, таблицы, задающие отношения двумерны. Одно измерение задается списком столбцов, второе измерение задается списком строк. Пара координат (Номер строки, Номер столбца) однозначно идентифицирует ячейку таблицы и содержащееся в ней значение. Если же допустить, что в ячейке таблицы могут содержаться данные сложных типов (массивы, структуры, другие таблицы), то такая таблица будет уже не плоской. Например, если в ячейке таблицы содержится массив, то для обращения к элементу массива нужно знать три параметра (Номер строки, Номер столбца, номер элемента в массиве).

Таким образом появляется третье объяснение Первой Нормальной Формы:

Объяснение 3. Отношение 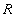находится в 1НФ, если оно является плоской таблицей.

Мы сознательно ограничиваемся рассмотрением только классической реляционной теории, в которой все отношения имеют только атомарные атрибуты и заведомо находятся в 1НФ.